GIS-Grundlagen in der Stadt- und Raumplanung Aufgabe 1
am Montag, 3. Mai 2010, 14:47
Aufgaben Teil 1) "Antworten"
1. Was ist das Gauß-Krüger-System (GK-System)?
Das Gauß-Krüger-Koordinatensystem ist ein kartesisches Koordinatensystem, das es ermöglicht, hinreichend kleine Gebiete der Erde mit metrischen Koordinaten (Rechtswert und Hochwert) konform zu verorten.
Das System wurde von Carl Friedrich Gauß und Johann Heinrich Louis Krüger entwickelt und wird vor allem im deutschsprachigen Raum seit 1923 genutzt Sehr viele amtliche topografische Kartenwerke, insbesondere großer und mittlerer Maßstäbe, bauen auf dem Gauß-Krüger-Koordinatensystem auf. Das Gauß-Krüger-System gehört der Gattung der transversalen Mercatorprojektion an.
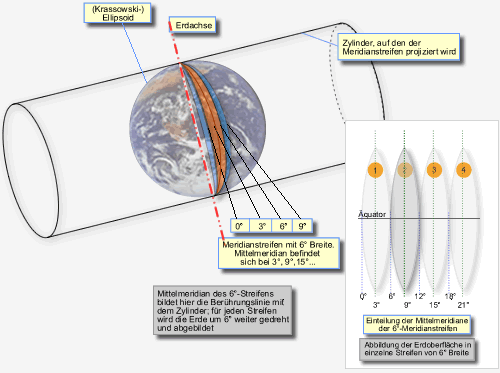
Gauß-Krüger-Koordinaten sind auf das System gelegte ebene, rechtwinklige Koordinaten. Sie werden (meist) 7-stellig als metrische Werte (in Metern) angegeben. Die Erde wird in 3° breite Meridianstreifen aufgeteilt (eine Einteilung in 6° wird auch angewendet). Das heißt, jeder Meridianstreifen geht vom Nord- bis zum Südpol und seine begrenzenden Meridiane liegen genau 3° auseinander. In der Mitte des Meridianstreifens verläuft der Mittelmeridian.
Jeder Meridianstreifen erhält eine Kennziffer. Diese leitet sich nach der klassischen Festlegung aus den ganzzahligen Vielfachen von 3° für den Mittelmeridian ab (0°, 3°, 6°,...):
Kennziffer = {0°, 3°, 6°, ... , 351°, 354°, 357°} / 3.
Um zu den Koordinaten eines Punktes innerhalb eines Meridianstreifens zu kommen, wird durch den in die Ebene projizierten Meridianstreifen am Äquator die Y-Achse gelegt und auf den längentreuen Mittelmeridian die X-Achse. X- und Y-Achse stehen senkrecht aufeinander, und man liest die Y- und X-Werte wie in einem kartesischen Koordinatensystem ab, also parallel zu den Achsen und nicht zu den jetzt bogenförmig verlaufenden Linien der Längen- und Breitengrade.
Der Y- und X-Wert wird in Metern angegeben. So gibt der X-Wert die Entfernung vom Äquator auf dem längentreu abgebildeten Mittelmeridian bis zum Ordinatenfußpunkt und der Y-Wert die Entfernung vom Mittelmeridian bis zum Punkt an. Um negative Werte bei den Y-Werten zu vermeiden, wird zu diesem Wert i.d.R. ein konstanter Wert von 500000 m addiert (nicht jedoch z.B. in Österreich).
Der X-Wert kann direkt als Hochwert der Gauß-Krüger-Koordinate ausgegeben werden. Dem Y-Wert wird noch die Kennziffer des Mittelmeridians vorangeschrieben und man erhält den Rechtswert des Punktes. Bei der Nennung von Koordinaten werden diese immer in der Reihenfolge Koordinatenrechtswert und Koordinatenhochwert angegeben, unabhängig vom Koordinatensystem (GK(RW,HW), UTM(E,N), geograph.(L,B), Photogrammetrie(x,y)). m zu den Koordinaten eines Punktes innerhalb eines Meridianstreifens zu kommen, wird durch den in die Ebene projizierten Meridianstreifen am Äquator die Y-Achse gelegt und auf den längentreuen Mittelmeridian die X-Achse. X- und Y-Achse stehen senkrecht aufeinander, und man liest die Y- und X-Werte wie in einem kartesischen Koordinatensystem ab, also parallel zu den Achsen und nicht zu den jetzt bogenförmig verlaufenden Linien der Längen- und Breitengrade.
Der Y- und X-Wert wird in Metern angegeben. So gibt der X-Wert die Entfernung vom Äquator auf dem längentreu abgebildeten Mittelmeridian bis zum Ordinatenfußpunkt und der Y-Wert die Entfernung vom Mittelmeridian bis zum Punkt an. Um negative Werte bei den Y-Werten zu vermeiden, wird zu diesem Wert i.d.R. ein konstanter Wert von 500000 m addiert.
2. Um welche Einheiten handelt es sich bei GK-Koordinaten?
Gauß-Krüger-Koordinaten sind ebene rechtwinklige Koordinaten, die aus Rechts- und Hochwert (zweidimensional) bestehen.
Die Erdoberfläche - annähernd eine Kugel - muss in eine Ebene abgebildet werden. Hierbei sollen die Längen-, Winkel- und Flächentreue möglichst gewahrt bleiben. Zur Vermeidung störender Abbildungsverzerrungen auf die Gauß-Krüger-Abbildungsebene dürfen die Rechtswerte bestimmte Beträge nicht überschreiten. Es wurden daher Abbildungsstreifen mit einer seitlichen Ausdehnung von drei Längengraden (Meridianstreifen) festgelegt. Der Rechtswert ist dann der senkrechte Abstand vom Mittelmeridian des Abbildungsstreifens. Um negative Koordinatenwerte zu vermeiden, erhält der Mittelmeridian einen festen Rechtswert von 500 km. Der Hochwert ist der Abstand des Punktes vom Äquator, gemessen entlang des Mittelmeridians.
3. Was ist ein Ellipsoid und welcher wird beim GK-System verwendet?
Ein Ellipsoid ist die höherdimensionale Entsprechung einer Ellipse.
Ein Ellipsoid ist der Graph der Relation x²/a²+y²/b²+z²/c²=1, dargestellt im kartesischen Koordinatensystem.
Der größtmögliche Definitionsbereich ist
D={(x, y, z)|-a<= x <=a, -b<= y <=b, -c<= z <=c}
Das Bessel-Ellipsoid (auch Bessel 1841) ist ein wichtiges Referenzellipsoid für Europa. Friedrich Wilhelm Bessel hat es 1841 aus den Daten großräumiger Vermessungen in Europa, Russland, Indien und Peru abgeleitet.
Das von Bessel verarbeitete Datenmaterial umfasst zehn lange Meridianbögen und 38 präzise Messungen der geografischen Breite und teilweise Länge.
In der deutschen Kartografie und Geodäsie wird dabei u.a. das Bessel-Ellipsoid genutzt.
4. Welche Projektionsart liegt dem Gauß-Krüger-System zugrunde
Das Gauß-Krüger-System gehört der Gattung der transversalen Mercatorprojektion an.
Die Mercator-Projektion in der Kartografie leitet sich aus der Zylinderprojektion ab, wobei die Projektion entlang der Zylinderachse – also in Nord-Süd-Richtung – geeignet verzerrt ist, um eine winkeltreue Abbildung zu erreichen. Gleichzeitig wird aber eine starke Flächenverzerrung in den Polarregionen in Kauf genommen. Insbesondere die Schifffahrt benutzt in den Seekarten diese winkelkorrigierte Darstellung der Erdoberfläche zur Navigation.
Sie wurde nach ihrem Erfinder, dem Kartografen Gerhard Mercator benannt.
5. Worin besteht der Unterschied zwischen geographischen und
projizierten, kartesischen Koordinaten?
Mit den geographischen Koordinaten (geographische Breite und geographische Länge) lässt sich die Lage eines Punktes auf der Erde beschreiben. Die Erde wird dabei in 360 Längengrade und 180 Breitengrade aufgeteilt.
Das Gradnetz der Erde ist ein gedachtes Koordinatensystem auf der Erdoberfläche mit sich rechtwinklig schneidenden Längen- und Breitenkreisen. Es dient zur geographischen Ortsbestimmung, das heißt, zur Festlegung des eigenen Standorts. Die Breitengrade werden dabei vom Äquator aus gezählt, die Pole liegen bei 90° Nord bzw. Süd, die Längengrade werden von einem willkürlichen Nullmeridian nach Osten und Westen gezählt bis jeweils 180°. Die Festlegung der Winkel ist dem in der Mathematik üblichen Kugelkoordinatensystem entgegengesetzt.
Bis Anfang des 20. Jahrhunderts waren in verschiedenen Ländern unterschiedliche Nullmeridiane gebräuchlich (z.B. der Ferro-Meridian von El Hierro und der Meridian von Paris), heute wird weltweit der Meridian von Greenwich (Sternwarte in London) verwendet.
Bei der genauen Ortsbestimmung muss beachtet werden, dass die Erde keine Kugel, sondern annähernd ein Ellipsoid ist, was Ortsverschiebungen bis 20 km bewirken könnte
Ein kartesisches Koordinatensystem ist ein orthogonales Koordinatensystem. Es ist nach dem latinisierten Namen Cartesius seines Erfinders René Descartes benannt. Im zwei- und dreidimensionalen Raum handelt es sich um das am häufigsten verwendete Koordinatensystem, da sich viele geometrische Sachverhalte in diesem am besten beschreiben lassen.
Ein Punkt wird über die Entfernung vom Ursprung/ Nullpunkt des Koordinatensystems definiert. Beim Kartesischen Koordinatensystem stehen die Koordinatenachsen senkrecht zueinander (2D: x- und y-Achse, 3D: x-, y- und z-Achse). Kartesische Koordinaten drücken den Standort zwei- oder dreidimensional als senkrechte Entfernung von zwei oder drei orthogonalen Achsen aus.
6.Warum werden im GK-System sog. Meridianstreifen verwendet?
Um die mit wachsendem Abstand vom Hauptmeridian größer werdenden Längen- und Flächenverzerrungen in praktisch annehmbaren Grenzen zu halten, beschränkte man in Deutschland die Gaußschen Systeme auf 3 -breite Meridianstreifen.
7.Wie erkennt man die Kennziffer des verwendeten Meridianstreifens an einer Koordinate?
Die Ordinaten (Rechtswerte y) zählen vom Hauptmeridian nach Osten positiv. Zur Vermeidung negativer Werte nach Westen erhält der Hauptmeridian den Rechtswert 500 000 m zugeordnet. Außerdem erhält der Rechtswert eine „Kennziffer“ (1, 2, 3,...), die den Meridianstreifen anzeigt.
Aufgaben Teil 2) "Dokumentation der Vorgehensweise"
Aufgabenstellung:
Auf der Grundlage der Topograpischen Karte 100 waren folgende Inhalte darzustellen:
1. Verwaltungsgrenzen für Landkreise, Verwaltungsgrenzen und Ortsgemeinden in verschiedenen
Umrandungsfarben und –stärken.
Umrandungsstärken waren <2>, <1>, und <0,5>.
Darstellung der LK in unterschiedlichen Farben.
2. Naturschutzgebiete mit grüner Umrandung in der Stärke 2 und gleichfarbiger Diagonalschraffur.
3. Beschriftungen der Ortsgemeinden und Naturschutzgebiete nach ihren Namen.
Layernamen umbenennen in:
Topograpische Karte 100, Ortsgemeinden, Verbandsgemeinden, Landkreise, Naturschutzgebiete
4. Erzeugen Sie eine Graphikdatei (Dateiformat ‚png’) für den räumlichen Umfang derVerbandsgemeinde Weilerbach mit dem Dateinamen ‚__uebung_1.png’
im Verzeichnis ‚\Abgaben\Uebung_1’.
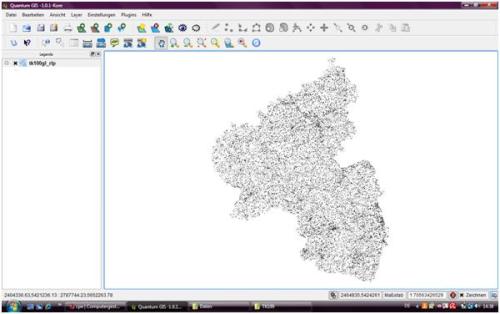
Schritt 1)"Rasterlayer laden"
Zuerst wurde die topographische Karte von Rheinland Pfalz als Basis geladen.
dies erfolgte über die Funktion Rasterlayer hinzufügen.
Rasterdaten laden
\Daten\TK100\TK100_RLP.tif
Rasterdatenquelle auswählen und öffnen
Bild " Rasterlayer"
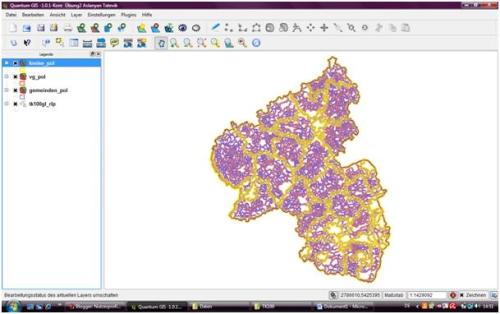
Schritt2)"Hinzufügen der verschiedenen Vektorenlayer"
Als zweiter Schritt wurden die Unterschiedlichen Vektorenlayer wie Ortsgemeinden, Verbandsgemeinden und Landkreise eingefügt.
Beispielsweise:
Vektordaten laden
\Daten\Verwaltungsgrenzen\Gemeinden.shp
Vektorlayer hinzufügen
Kodierung auf ‚System’ oder ‚CP1252’ und der
Dateityp auf ‚[OGR] ESRI Shapefile’ eingestellt.
Bild "Vektorenlayer"
"Beschriftungen, Umrandungsstärke, Farbgebung"
Danach wurde die Vektorenlayer entsprechend der Vorgaben bearbeitet, Farbgebung, Umrandungsstärke und Beschriftung erfolgten über die Eigenschaften der Layer, Beschriftung bzw. Darstellung.
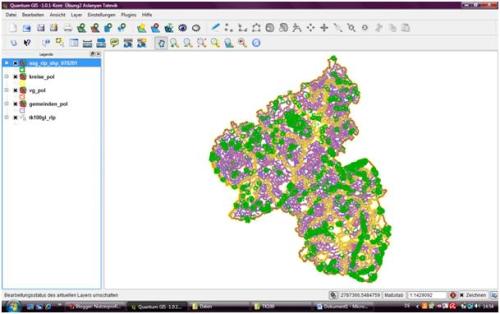
Schritt 3 ) Einfügen der Naturschutzkarte
Als dritter Schritt wurde ebenfalls über die Funktion Vektorenlayer hinzufügen, die Naturschutzgebiete eingefügt.
Über die Layereigenschaften/Darstellung wurden die vorgeschriebenen Einstellungen wie Farbgebung bzw. Strichstärke, Schraffierung vorgenommen.
Bild " Naturschutzgebiete"
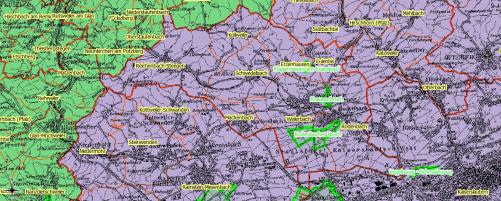
Schritt 4) Erzeugen der Graphikdatei, Bereich Weilerbach,
Ordnen der Layer
Danach wurde die Layerreihenfolge geändert. Dies war mittels
Drag and Drop möglich.
Die Layer wurden entsprechend der Vorgaben umbenannt. (Layernamen)
Zuletzt wurde der Bereich "Weilerbach mit Hilfe der Attributtabelle "verortet/ gezoomt" und
der aktuellen Kartenanzeigen Bereich Weilerbach als png Graphikdatei gespeichert.
Bild " png Graphikdatei"
1. Was ist das Gauß-Krüger-System (GK-System)?
Das Gauß-Krüger-Koordinatensystem ist ein kartesisches Koordinatensystem, das es ermöglicht, hinreichend kleine Gebiete der Erde mit metrischen Koordinaten (Rechtswert und Hochwert) konform zu verorten.
Das System wurde von Carl Friedrich Gauß und Johann Heinrich Louis Krüger entwickelt und wird vor allem im deutschsprachigen Raum seit 1923 genutzt Sehr viele amtliche topografische Kartenwerke, insbesondere großer und mittlerer Maßstäbe, bauen auf dem Gauß-Krüger-Koordinatensystem auf. Das Gauß-Krüger-System gehört der Gattung der transversalen Mercatorprojektion an.
Gauß-Krüger-Koordinaten sind auf das System gelegte ebene, rechtwinklige Koordinaten. Sie werden (meist) 7-stellig als metrische Werte (in Metern) angegeben. Die Erde wird in 3° breite Meridianstreifen aufgeteilt (eine Einteilung in 6° wird auch angewendet). Das heißt, jeder Meridianstreifen geht vom Nord- bis zum Südpol und seine begrenzenden Meridiane liegen genau 3° auseinander. In der Mitte des Meridianstreifens verläuft der Mittelmeridian.
Jeder Meridianstreifen erhält eine Kennziffer. Diese leitet sich nach der klassischen Festlegung aus den ganzzahligen Vielfachen von 3° für den Mittelmeridian ab (0°, 3°, 6°,...):
Kennziffer = {0°, 3°, 6°, ... , 351°, 354°, 357°} / 3.
Um zu den Koordinaten eines Punktes innerhalb eines Meridianstreifens zu kommen, wird durch den in die Ebene projizierten Meridianstreifen am Äquator die Y-Achse gelegt und auf den längentreuen Mittelmeridian die X-Achse. X- und Y-Achse stehen senkrecht aufeinander, und man liest die Y- und X-Werte wie in einem kartesischen Koordinatensystem ab, also parallel zu den Achsen und nicht zu den jetzt bogenförmig verlaufenden Linien der Längen- und Breitengrade.
Der Y- und X-Wert wird in Metern angegeben. So gibt der X-Wert die Entfernung vom Äquator auf dem längentreu abgebildeten Mittelmeridian bis zum Ordinatenfußpunkt und der Y-Wert die Entfernung vom Mittelmeridian bis zum Punkt an. Um negative Werte bei den Y-Werten zu vermeiden, wird zu diesem Wert i.d.R. ein konstanter Wert von 500000 m addiert (nicht jedoch z.B. in Österreich).
Der X-Wert kann direkt als Hochwert der Gauß-Krüger-Koordinate ausgegeben werden. Dem Y-Wert wird noch die Kennziffer des Mittelmeridians vorangeschrieben und man erhält den Rechtswert des Punktes. Bei der Nennung von Koordinaten werden diese immer in der Reihenfolge Koordinatenrechtswert und Koordinatenhochwert angegeben, unabhängig vom Koordinatensystem (GK(RW,HW), UTM(E,N), geograph.(L,B), Photogrammetrie(x,y)). m zu den Koordinaten eines Punktes innerhalb eines Meridianstreifens zu kommen, wird durch den in die Ebene projizierten Meridianstreifen am Äquator die Y-Achse gelegt und auf den längentreuen Mittelmeridian die X-Achse. X- und Y-Achse stehen senkrecht aufeinander, und man liest die Y- und X-Werte wie in einem kartesischen Koordinatensystem ab, also parallel zu den Achsen und nicht zu den jetzt bogenförmig verlaufenden Linien der Längen- und Breitengrade.
Der Y- und X-Wert wird in Metern angegeben. So gibt der X-Wert die Entfernung vom Äquator auf dem längentreu abgebildeten Mittelmeridian bis zum Ordinatenfußpunkt und der Y-Wert die Entfernung vom Mittelmeridian bis zum Punkt an. Um negative Werte bei den Y-Werten zu vermeiden, wird zu diesem Wert i.d.R. ein konstanter Wert von 500000 m addiert.
2. Um welche Einheiten handelt es sich bei GK-Koordinaten?
Gauß-Krüger-Koordinaten sind ebene rechtwinklige Koordinaten, die aus Rechts- und Hochwert (zweidimensional) bestehen.
Die Erdoberfläche - annähernd eine Kugel - muss in eine Ebene abgebildet werden. Hierbei sollen die Längen-, Winkel- und Flächentreue möglichst gewahrt bleiben. Zur Vermeidung störender Abbildungsverzerrungen auf die Gauß-Krüger-Abbildungsebene dürfen die Rechtswerte bestimmte Beträge nicht überschreiten. Es wurden daher Abbildungsstreifen mit einer seitlichen Ausdehnung von drei Längengraden (Meridianstreifen) festgelegt. Der Rechtswert ist dann der senkrechte Abstand vom Mittelmeridian des Abbildungsstreifens. Um negative Koordinatenwerte zu vermeiden, erhält der Mittelmeridian einen festen Rechtswert von 500 km. Der Hochwert ist der Abstand des Punktes vom Äquator, gemessen entlang des Mittelmeridians.
3. Was ist ein Ellipsoid und welcher wird beim GK-System verwendet?
Ein Ellipsoid ist die höherdimensionale Entsprechung einer Ellipse.
Ein Ellipsoid ist der Graph der Relation x²/a²+y²/b²+z²/c²=1, dargestellt im kartesischen Koordinatensystem.
Der größtmögliche Definitionsbereich ist
D={(x, y, z)|-a<= x <=a, -b<= y <=b, -c<= z <=c}
Das Bessel-Ellipsoid (auch Bessel 1841) ist ein wichtiges Referenzellipsoid für Europa. Friedrich Wilhelm Bessel hat es 1841 aus den Daten großräumiger Vermessungen in Europa, Russland, Indien und Peru abgeleitet.
Das von Bessel verarbeitete Datenmaterial umfasst zehn lange Meridianbögen und 38 präzise Messungen der geografischen Breite und teilweise Länge.
In der deutschen Kartografie und Geodäsie wird dabei u.a. das Bessel-Ellipsoid genutzt.
4. Welche Projektionsart liegt dem Gauß-Krüger-System zugrunde
Das Gauß-Krüger-System gehört der Gattung der transversalen Mercatorprojektion an.
Die Mercator-Projektion in der Kartografie leitet sich aus der Zylinderprojektion ab, wobei die Projektion entlang der Zylinderachse – also in Nord-Süd-Richtung – geeignet verzerrt ist, um eine winkeltreue Abbildung zu erreichen. Gleichzeitig wird aber eine starke Flächenverzerrung in den Polarregionen in Kauf genommen. Insbesondere die Schifffahrt benutzt in den Seekarten diese winkelkorrigierte Darstellung der Erdoberfläche zur Navigation.
Sie wurde nach ihrem Erfinder, dem Kartografen Gerhard Mercator benannt.
5. Worin besteht der Unterschied zwischen geographischen und
projizierten, kartesischen Koordinaten?
Mit den geographischen Koordinaten (geographische Breite und geographische Länge) lässt sich die Lage eines Punktes auf der Erde beschreiben. Die Erde wird dabei in 360 Längengrade und 180 Breitengrade aufgeteilt.
Das Gradnetz der Erde ist ein gedachtes Koordinatensystem auf der Erdoberfläche mit sich rechtwinklig schneidenden Längen- und Breitenkreisen. Es dient zur geographischen Ortsbestimmung, das heißt, zur Festlegung des eigenen Standorts. Die Breitengrade werden dabei vom Äquator aus gezählt, die Pole liegen bei 90° Nord bzw. Süd, die Längengrade werden von einem willkürlichen Nullmeridian nach Osten und Westen gezählt bis jeweils 180°. Die Festlegung der Winkel ist dem in der Mathematik üblichen Kugelkoordinatensystem entgegengesetzt.
Bis Anfang des 20. Jahrhunderts waren in verschiedenen Ländern unterschiedliche Nullmeridiane gebräuchlich (z.B. der Ferro-Meridian von El Hierro und der Meridian von Paris), heute wird weltweit der Meridian von Greenwich (Sternwarte in London) verwendet.
Bei der genauen Ortsbestimmung muss beachtet werden, dass die Erde keine Kugel, sondern annähernd ein Ellipsoid ist, was Ortsverschiebungen bis 20 km bewirken könnte
Ein kartesisches Koordinatensystem ist ein orthogonales Koordinatensystem. Es ist nach dem latinisierten Namen Cartesius seines Erfinders René Descartes benannt. Im zwei- und dreidimensionalen Raum handelt es sich um das am häufigsten verwendete Koordinatensystem, da sich viele geometrische Sachverhalte in diesem am besten beschreiben lassen.
Ein Punkt wird über die Entfernung vom Ursprung/ Nullpunkt des Koordinatensystems definiert. Beim Kartesischen Koordinatensystem stehen die Koordinatenachsen senkrecht zueinander (2D: x- und y-Achse, 3D: x-, y- und z-Achse). Kartesische Koordinaten drücken den Standort zwei- oder dreidimensional als senkrechte Entfernung von zwei oder drei orthogonalen Achsen aus.
6.Warum werden im GK-System sog. Meridianstreifen verwendet?
Um die mit wachsendem Abstand vom Hauptmeridian größer werdenden Längen- und Flächenverzerrungen in praktisch annehmbaren Grenzen zu halten, beschränkte man in Deutschland die Gaußschen Systeme auf 3 -breite Meridianstreifen.
7.Wie erkennt man die Kennziffer des verwendeten Meridianstreifens an einer Koordinate?
Die Ordinaten (Rechtswerte y) zählen vom Hauptmeridian nach Osten positiv. Zur Vermeidung negativer Werte nach Westen erhält der Hauptmeridian den Rechtswert 500 000 m zugeordnet. Außerdem erhält der Rechtswert eine „Kennziffer“ (1, 2, 3,...), die den Meridianstreifen anzeigt.

Aufgaben Teil 2) "Dokumentation der Vorgehensweise"
Aufgabenstellung:
Auf der Grundlage der Topograpischen Karte 100 waren folgende Inhalte darzustellen:
1. Verwaltungsgrenzen für Landkreise, Verwaltungsgrenzen und Ortsgemeinden in verschiedenen
Umrandungsfarben und –stärken.
Umrandungsstärken waren <2>, <1>, und <0,5>.
Darstellung der LK in unterschiedlichen Farben.
2. Naturschutzgebiete mit grüner Umrandung in der Stärke 2 und gleichfarbiger Diagonalschraffur.
3. Beschriftungen der Ortsgemeinden und Naturschutzgebiete nach ihren Namen.
Layernamen umbenennen in:
Topograpische Karte 100, Ortsgemeinden, Verbandsgemeinden, Landkreise, Naturschutzgebiete
4. Erzeugen Sie eine Graphikdatei (Dateiformat ‚png’) für den räumlichen Umfang derVerbandsgemeinde Weilerbach mit dem Dateinamen ‚__uebung_1.png’
im Verzeichnis ‚\Abgaben\Uebung_1’.
Schritt 1)"Rasterlayer laden"
Zuerst wurde die topographische Karte von Rheinland Pfalz als Basis geladen.
dies erfolgte über die Funktion Rasterlayer hinzufügen.
Rasterdaten laden
\Daten\TK100\TK100_RLP.tif
Rasterdatenquelle auswählen und öffnen
Bild " Rasterlayer"

Schritt2)"Hinzufügen der verschiedenen Vektorenlayer"
Als zweiter Schritt wurden die Unterschiedlichen Vektorenlayer wie Ortsgemeinden, Verbandsgemeinden und Landkreise eingefügt.
Beispielsweise:
Vektordaten laden
\Daten\Verwaltungsgrenzen\Gemeinden.shp
Vektorlayer hinzufügen
Kodierung auf ‚System’ oder ‚CP1252’ und der
Dateityp auf ‚[OGR] ESRI Shapefile’ eingestellt.
Bild "Vektorenlayer"

"Beschriftungen, Umrandungsstärke, Farbgebung"
Danach wurde die Vektorenlayer entsprechend der Vorgaben bearbeitet, Farbgebung, Umrandungsstärke und Beschriftung erfolgten über die Eigenschaften der Layer, Beschriftung bzw. Darstellung.
Schritt 3 ) Einfügen der Naturschutzkarte
Als dritter Schritt wurde ebenfalls über die Funktion Vektorenlayer hinzufügen, die Naturschutzgebiete eingefügt.
Über die Layereigenschaften/Darstellung wurden die vorgeschriebenen Einstellungen wie Farbgebung bzw. Strichstärke, Schraffierung vorgenommen.
Bild " Naturschutzgebiete"

Schritt 4) Erzeugen der Graphikdatei, Bereich Weilerbach,
Ordnen der Layer
Danach wurde die Layerreihenfolge geändert. Dies war mittels
Drag and Drop möglich.
Die Layer wurden entsprechend der Vorgaben umbenannt. (Layernamen)
Zuletzt wurde der Bereich "Weilerbach mit Hilfe der Attributtabelle "verortet/ gezoomt" und
der aktuellen Kartenanzeigen Bereich Weilerbach als png Graphikdatei gespeichert.
Bild " png Graphikdatei"
